Activities and Exercises Part 5: The Conceptual Math Tables
The Conceptual Math table is a way for students to see the patterns repeating within the multiples of a chosen number. The students need to create their own tables for this, not have them given to the prepared. These tables should then be kept in a special folder or portfolio.
Depending on your group, I would start with 2s or 3s. I like to spend time with the even numbers as a way for students to familiarize themselves with the basic fact that all even numbers can only create even numbers in their multiplication table. Generally, it is good to have students chart the 2s. However, some students will become frustrated or angry if they feel the work is “too easy” or “baby”, and if this is the case you can allow students to work with a number of their choice. I usually do this, and I find they will often come back to the twos. You can also give them a grid to fill in with the primes only. Using stickers or some other way for them to monitor their progress is good. Teaching them to keep tabs on their own learning is a way to build connection to the content.
Once students get to larger numbers, even with the 2s they tend to make mistakes. One of the biggest obstacles I have seen is when students see larger numbers, they haven’t gone that high and start to do strange things with the place values.
Exposing the students to larger numbers sooner is better for them. Doing it in this simple sequential way creates a deeper understanding of the relative size of the place-value change. When they move up sequentially, they experience it. If you just have them jump up to high numbers from double digits, they haven’t experienced it conceptually.
Please be prepared to provide them as many sheets as they need to be able to complete the sequence correctly. Once they have the sequence down, you can give them a large poster board to complete.
Within the multiples of 2, are represented all of the multiples of 4, all of the multiples of 6, all of the multiples of 8, etc. This is something that is a critical underlying assumption that students should develop within the Conceptual Math system. This is understood as the basis for higher level concepts, it can be introduced with these concepts.
Charting the Primes
Tables should be done in Primes. The tables themselves are a way to introduce the idea of primes and factors. The tables can also be used for equivalent fractions, but that is for another book.
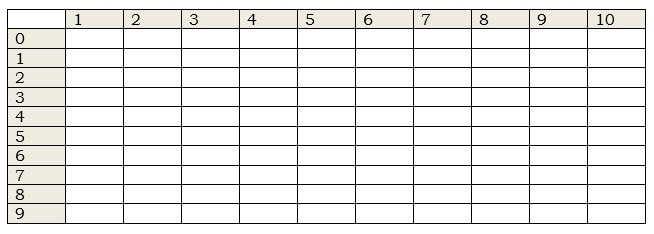
Table 1. This is what a typical blank table looks like. Ones values are across the top, and tens values are on the left.
The numbers on the top represent the ones place and the numbers on the left represent the tens place values. It is useful to write ONES across the top, and TENS across the side. This can just be written without explanation, or if verbalized is should be done as a simple statement of fact. Those who are ready will pick it up, and those who are not won’t get frustrated and shut down if you do this gently.
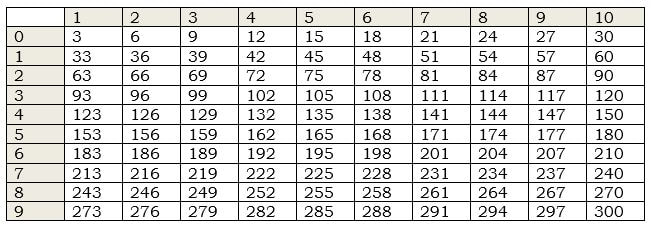
Table 2. A partially filled in table for the twos.
Table 2. A partially filled in table for the twos.
As the students start to fill in the table they start to recognize some patterns.
Students might say, “The end numbers are repeating.”
They might point out, “The five always ends in zero.”
Or they might start noticing patterns in the tens place, like the fives are always odd, and the 10 is always even.
Once the chart is complete give them some time to look for the patterns. If you have a group and are letting them complete the charts independently, have them show you so you can check their work. You can ask them to show you some patterns. Then let them move on to the threes. Make sure they are using pencil, and that you check their work. Especially watch that they do not jump up in the 100s place. Place value mistakes are common. Emphasize that we use pencil in math because it is OK to make mistakes when you have and eraser! We learn more from our mistakes than when we do everything right. It is neurobiology at work.
Students might say, “The end numbers are repeating.”
They might point out, “The five always ends in zero.”
Or they might start noticing patterns in the tens place, like the fives are always odd, and the 10 is always even.
Once the chart is complete give them some time to look for the patterns. If you have a group and are letting them complete the charts independently, have them show you so you can check their work. You can ask them to show you some patterns. Then let them move on to the threes. Make sure they are using pencil, and that you check their work. Especially watch that they do not jump up in the 100s place. Place value mistakes are common. Emphasize that we use pencil in math because it is OK to make mistakes when you have and eraser! We learn more from our mistakes than when we do everything right. It is neurobiology at work.
Before you read on, take a minute to look at the chart. See what patterns you notice.
Maybe you noticed that all the ones values repeat the core sequence:
1 is ALWAYS 3, 2 is ALWAYS 6, 3 is ALWAYS 9,
4 is always 2, 5 is always 5, 6 is always 8
7 is always 1, 8 is always 4, 9 is always 7 and of course 10 is always 0.
Did you notice that if you read down the tens place values, our core patterns repeat as well? Go look.
And they repeat in our clusters of three. So for 1, 2, 3. It is 3_, 6_, 9_, in the tens place going down. Followed by (1)2_, (1)5_, (1)8_, and the (2)1_, (2)4_, (2)7_.
Maybe you noticed that all the ones values repeat the core sequence:
1 is ALWAYS 3, 2 is ALWAYS 6, 3 is ALWAYS 9,
4 is always 2, 5 is always 5, 6 is always 8
7 is always 1, 8 is always 4, 9 is always 7 and of course 10 is always 0.
Did you notice that if you read down the tens place values, our core patterns repeat as well? Go look.
And they repeat in our clusters of three. So for 1, 2, 3. It is 3_, 6_, 9_, in the tens place going down. Followed by (1)2_, (1)5_, (1)8_, and the (2)1_, (2)4_, (2)7_.
You students might then realize that the multiples of three are now showing up in order as they are related to what is in the first column of the table, the tens place.
The kids will notice even more things. They look on the diagonals. Some of them add or do other things with the numbers. It is a lot of fun.
I would work with the charts like this until all students had completed at least the twos and threes. Some of the kids will keep going up. You should let them. Some students may get many charts done before we go on to the next phase.
At this point you should assign only prime numbers. If a student asks to do the number four, for example, simply tell him we don’t need that number. If they ask why, tell them they will find out. This will plant the question, and the student will consciously/or subconsciously be seeking an answer for this question. You are “priming” their brain to talk about primes.
Highlighting the Second Order Multiples
After everyone has completed the twos and threes you are going to ask what numbers have been completed. Write them on the board. In a larger class, with the students working at their own pace, you likely will have accomplished all the prime numbers up to 11. The list should look like this.
2,3,5,7,11
Ask what numbers you skipped. This list will include these numbers.
4,6,8,9,10
You should have mentioned the word prime casually by this point and you may have it written in different places around the room. You are ready now to discuss the fact that primes are special numbers that can’t be broken down, and that every other number comes from primes.
You can then have them do the second part of the charts. Finding the second order multiples within the primes.
You should make a large poster-board of the twos and threes for this activity. It would be fine to have your students make large poster-boards also. I find working large helps them.
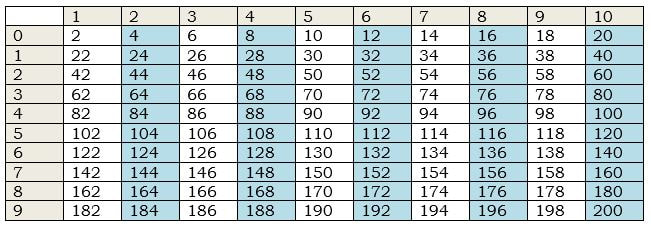
Charting the Multiples of Four in the Twos
*Have extra copies of completed twos charts to distribute if necessary.
Tell students to place their own twos table from their portfolio in front of them. Say we are going to find ALL of the multiples of four that we can in the twos.
Have the students do their multiples of four together. When stating the number, point to the multiple on the large size chart. Tell the student to point to the multiple of fours on their own twos table. If you want to emphasize the use of the base ten circle, you can invite one student to guide us up to 200. They will need to know the pattern for the fours. You may at this point have large posters of the patterns around the room, and simply have the student go to that poster to guide the class.
When finished, ask them what they noticed. They might notice that the fours skip every other square on the table. Now tell them we are going to put a square around each of the places where we saw a multiple of four.
Have the students work independently to put a square around each multiple of four. They will start to see the pattern in the multiples of four.
Table 4. The multiples of four are highlighted within the twos chart.
The kids will notice even more things. They look on the diagonals. Some of them add or do other things with the numbers. It is a lot of fun.
I would work with the charts like this until all students had completed at least the twos and threes. Some of the kids will keep going up. You should let them. Some students may get many charts done before we go on to the next phase.
At this point you should assign only prime numbers. If a student asks to do the number four, for example, simply tell him we don’t need that number. If they ask why, tell them they will find out. This will plant the question, and the student will consciously/or subconsciously be seeking an answer for this question. You are “priming” their brain to talk about primes.
Highlighting the Second Order Multiples
After everyone has completed the twos and threes you are going to ask what numbers have been completed. Write them on the board. In a larger class, with the students working at their own pace, you likely will have accomplished all the prime numbers up to 11. The list should look like this.
2,3,5,7,11
Ask what numbers you skipped. This list will include these numbers.
4,6,8,9,10
You should have mentioned the word prime casually by this point and you may have it written in different places around the room. You are ready now to discuss the fact that primes are special numbers that can’t be broken down, and that every other number comes from primes.
You can then have them do the second part of the charts. Finding the second order multiples within the primes.
You should make a large poster-board of the twos and threes for this activity. It would be fine to have your students make large poster-boards also. I find working large helps them.
Charting the Multiples of Four in the Twos
*Have extra copies of completed twos charts to distribute if necessary.
Tell students to place their own twos table from their portfolio in front of them. Say we are going to find ALL of the multiples of four that we can in the twos.
Have the students do their multiples of four together. When stating the number, point to the multiple on the large size chart. Tell the student to point to the multiple of fours on their own twos table. If you want to emphasize the use of the base ten circle, you can invite one student to guide us up to 200. They will need to know the pattern for the fours. You may at this point have large posters of the patterns around the room, and simply have the student go to that poster to guide the class.
When finished, ask them what they noticed. They might notice that the fours skip every other square on the table. Now tell them we are going to put a square around each of the places where we saw a multiple of four.
Have the students work independently to put a square around each multiple of four. They will start to see the pattern in the multiples of four.
Table 4. The multiples of four are highlighted within the twos chart.
For the sake of ease, I simply highlighted all of the multiples of four in blue. You may want to have made some copies of the twos for back-up, or practice.
Once they have completed this, you can say. Use this phrase, or one that is similar as a mantra. If you say this mantra enough, they will internalize it. They will make the connection on a deep level
MANTRA: “Do we have ALL of the multiples of four?” “Did we miss any?”
Always use the same phrase here, it will focus attention on this fact for the students and become automatic in their own thinking.
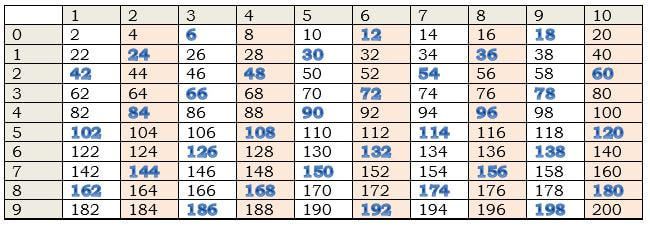
Charting the Multiples of Six in the Twos
Then we can go on. Ask, “What is the next number in our sequence?” “Let’s check if we have all of the multiples of 6 in our twos table.”
Have someone count by 6s, and first have them just point to the sixes as we go.
Let them decide if all of the sixes are there.
“OK class, let’s mark them.”
“Caps off”
Now mark each of the 6s with another shape. You can use a circle or triangle, or you can come up with your own marking system completely different than mine.
Below you see the chart marked with all of the multiples of six. I used a blue-bubble font, but you will use a shape of some sort, or some way to mark what they have already written. Remember you will have them continue with the multiples as far as they can handle, so try to make it not too busy.
Table 5. Highlighted second-order multiples of six and four.
Don’t forget the mantra.
Repeat the phrase: “Do we have ALL of the multiples of six?” “Did we miss any?”
The patterns in the six are more subtle, but many of the students will see a diagonal pattern. Check it out—what happens if you add the digits of each number on the diagonal.
Did you see the pattern?
6, (2+4)=6, (4+2)=6…
Can you make the 60 diagonal work?
60, 78, 96, 114, 132, 150…
Continue exploring the tables, and add more of the second order multiples. Get creative in your labelling. You do not want to lose your ability to see all the patterns.
I would try to go up to 10 for the twos. Five places is hard enough to see. If you want to have them do more, maybe break it down and let them do the values past 10 on a clean twos table.
Spend time with these. You can have them reference them for working with worksheets or other written work. It will help them to connect with the tables.
When they have done this completely and correctly, have them move on to the threes and the rest of the prime tables. Ultimately all of the students should finish the primes up to 11. This will take some students much longer than others. It doesn’t matter. Help them make goals and reach them.
All of their completed sheets should go into their own personal portfolio. You will come back to these charts over and over. A portfolio-based approach is one of the best ways to differentiate instruction and to have a record of each student’s work, showing both strengths and weaknesses, that goes far beyond what we can learn through testing.
Teachers should not be afraid to mention higher-level concepts like sets, union, factors, and other relevant terms. This should be done only if the teacher fully understands these terms, as a wrong introduction can have negative consequences, and is harder to unlearn than if the student is never exposed to the terms.
Repeat the phrase: “Do we have ALL of the multiples of six?” “Did we miss any?”
The patterns in the six are more subtle, but many of the students will see a diagonal pattern. Check it out—what happens if you add the digits of each number on the diagonal.
Did you see the pattern?
6, (2+4)=6, (4+2)=6…
Can you make the 60 diagonal work?
60, 78, 96, 114, 132, 150…
Continue exploring the tables, and add more of the second order multiples. Get creative in your labelling. You do not want to lose your ability to see all the patterns.
I would try to go up to 10 for the twos. Five places is hard enough to see. If you want to have them do more, maybe break it down and let them do the values past 10 on a clean twos table.
Spend time with these. You can have them reference them for working with worksheets or other written work. It will help them to connect with the tables.
When they have done this completely and correctly, have them move on to the threes and the rest of the prime tables. Ultimately all of the students should finish the primes up to 11. This will take some students much longer than others. It doesn’t matter. Help them make goals and reach them.
All of their completed sheets should go into their own personal portfolio. You will come back to these charts over and over. A portfolio-based approach is one of the best ways to differentiate instruction and to have a record of each student’s work, showing both strengths and weaknesses, that goes far beyond what we can learn through testing.
Teachers should not be afraid to mention higher-level concepts like sets, union, factors, and other relevant terms. This should be done only if the teacher fully understands these terms, as a wrong introduction can have negative consequences, and is harder to unlearn than if the student is never exposed to the terms.